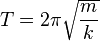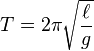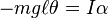An object moving along the x-axis is said to exhibit simple harmonic motion if its position as a function of time varies as
x(t) = x0 + Acos(ωt + φ).
The object oscillates about the equilibrium position x0. If we choose the origin of our coordinate system such that x0 = 0, then the displacement x from the equilibrium position as a function of time is given by
x(t) = Acos(ωt + φ).
A is the amplitude of the oscillation, i.e. the maximum displacement of the object from equilibrium, either in the positive or negative x-direction. Simple harmonic motion is repetitive. The periodT is the time it takes the object to complete one oscillation and return to the starting position. The angular frequency ω is given by ω = 2π/T. The angular frequency is measured in radians per second. The inverse of the period is the frequency f = 1/T. The frequency f = 1/T = ω/2π of the motion gives the number of complete oscillations per unit time. It is measured in units of Hertz, (1Hz = 1/s).
The velocity of the object as a function of time is given by
v(t) = dx(t)/dt = -ωAsin(ωt + φ),
and the acceleration is given by
a(t) = dv(t)/dt = -ω2Acos(ωt + φ) = -ω2x.
The quantity φ is called the phase constant. It is determined by the initial conditions of the motion. If at t = 0 the object has its maximum displacement in the positive x-direction, then φ = 0, if it has its maximum displacement in the negative x-direction, then φ = π. If at t = 0 the particle is moving through its equilibrium position with maximum velocity in the negative x-direction then φ = π/2. The quantity ωt + φ is called the phase.
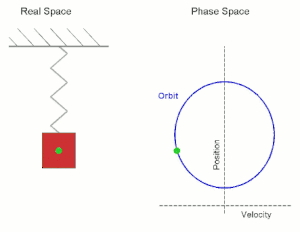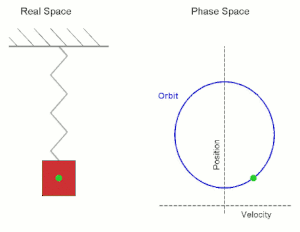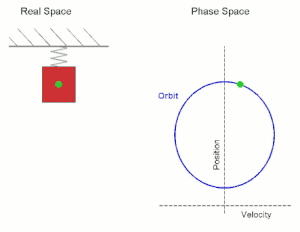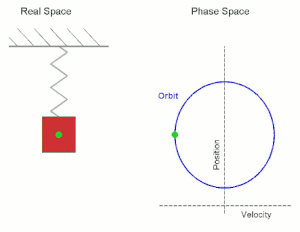
In the figure below position and velocity are plotted as a function of time for oscillatory motion with a period of 5 s. The amplitude and the maximum velocity have arbitrary units. Position and velocity are out of phase. The velocity is zero at maximum displacement, and the displacement is zero at maximum speed.

For simple harmonic motion, the acceleration a = -ω2x is proportional to the displacement, but in the opposite direction. Simple harmonic motion is accelerated motion. If an object exhibits simple harmonic motion, a force must be acting on the object. The force is
F = ma = -mω2x .
It obeys Hooke's law, F = -kx, with k = mω2.
F = ma = md2x/dt2 with F = -kx, leads to the second-order differential equation
d2x/dt2 = -(k/m)x.
We now know how to solve this equation. The solution is
x(t) = Acos(ωt + φ), with ω2 = k/m.
The solution to a second-order differential equation includes two constants of integration. Here these constants are A and φ. They are determined by the initial conditions of the problem.
The same equations have the same solutions. Whenever you encounter a differential equation of the form d2x/dt2 = -b2x, you know that the solution is x(t) = Acos(ωt + φ), with ω = b.
The force exerted by a spring obeys Hooke's law. Assume that an object is attached to a spring, which is stretched or compressed. Then the spring exerts a force on the object. This force is proportional to the displacement of the spring from its equilibrium position and is in a direction opposite to the displacement.
F = -kx
Assume the spring is stretched a distance A and then released. The object attached to the spring accelerates.
a = -(k/m)x
It gains speed as it moves towards the equilibrium position because its acceleration is in the direction of its velocity. When it is at the equilibrium position, the acceleration is zero, but the object has kinetic energy. It overshoots the equilibrium position and starts slowing down, because the acceleration is now in a direction opposite to the direction of its velocity. Neglecting friction, it comes to a stop when the spring is compressed by a distance A and then accelerates back towards the equilibrium position. It again overshoots and comes to a stop at the initial position when the spring is stretched a distance A. The motion repeats. The object oscillates back and forth. It executes simple harmonic motion. The angular frequency of the motion is
the period is
and the frequency is
Examples
The following physical systems are some examples of simple harmonic oscillator.
[edit]Mass on a spring
A mass m attached to a spring of spring constant k exhibits simple harmonic motion in closed space. The equation
shows that the period of oscillation is independent of both the amplitude and gravitational acceleration
[edit]Uniform circular motion
Simple harmonic motion can in some cases be considered to be the one-dimensional projection of uniform circular motion. If an object moves with angular velocity ωaround a circle of radius r centered at the origin of the x-y plane, then its motion along each coordinate is simple harmonic motion with amplitude r and angular frequencyω.
[edit]Mass on a simple pendulum
In the small-angle approximation, the motion of a simple pendulum is approximated by simple harmonic motion. The period of a mass attached to a pendulum of length ℓwith gravitational acceleration g is given by
This shows that the period of oscillation is independent of the amplitude and mass of the pendulum but not the acceleration due to gravity (g), therefore a pendulum of the same length on the Moon would swing more slowly due to the Moon's lower gravitational acceleration.
This approximation is accurate only in small angles because of the expression for angular acceleration α being proportional to the sine of position:
where I is the moment of inertia. When θ is small, sin θ ≈ θ and therefore the expression becomes
which makes angular acceleration directly proportional to θ, satisfying the definition of simple harmonic motion.